CNN의 기본적인 구조 및 원리 - 1

처음 회사에서 인공지능 업무를 배정받기 이전에, 기본적인 CNN 구조에 대해 확실히 알고 가야 제대로 활용할 수 있겠다는 이야기를 듣고 CNN 구조부터 확실히 짚어가기 위해 기본적인 구조에 대한 학습을 시작했다. 이 포스트는 사내에서 세미나를 진행했던 CNN 기초를 다시 복습할 겸 저장하는 블로그 글이다. 사실 세미나를 진행한 시기는 올해 초이기 때문에 굉장히 오래됐고, 글 자체도 그 때 당시에 정리했던 ppt나 노션 등을 나름 잘 정리해서 적어보는 글인데, 누락된 부분이나 잘못 적거나 부실하게 설명한 부분이 있을 수 있다. (그런 부분들에 대해서는 댓글로 지적해주시면 수정하도록 하겠습니다!)

Perceptron

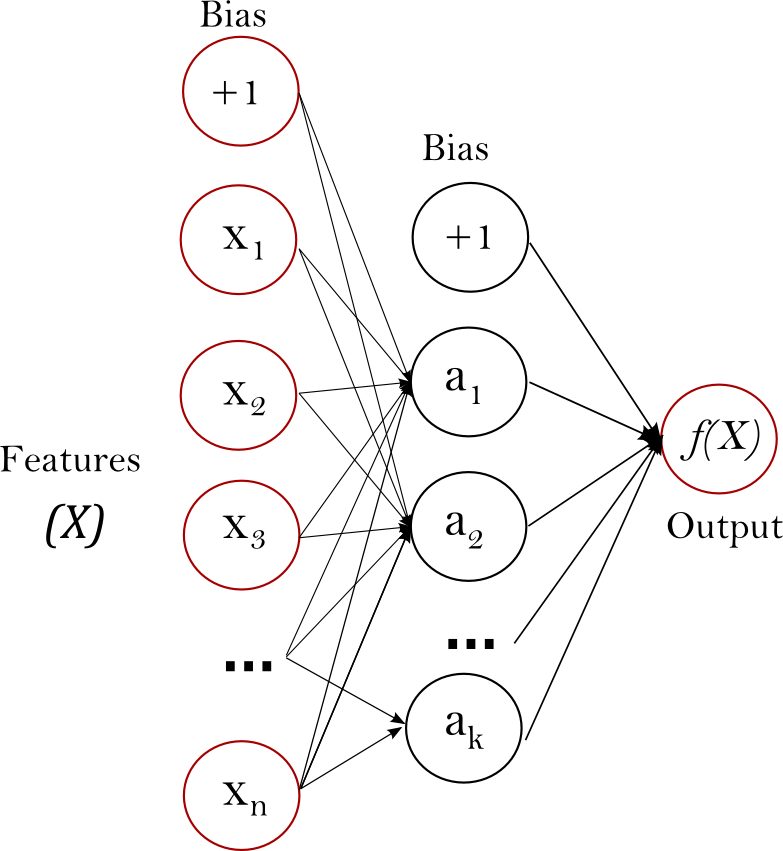CNN이 본격적으로 활용되기 이전에 뉴럴 네트워크를 통해 image classification 등의 문제를 풀 때는 주로 perceptron 구조를 사용했다. 특정 차원의 벡터로 이루어진 입력이 들어오면 이 것을 여러 층의 hidden layer를 거쳐 출력 값을 내놓는 구조가 Multi layer perceptron이다. 여기서 이 다중 레이어의 퍼셉트론이라는 구조가 왜 나왔는지가 중요한데, 우리가 일반적으로 선형 함수로 되어 있는 특정 문제를 풀기 위해서는 단일 레이어내에 정의된 함수를 통과하면 원하는 값을 도출할 수 있을 것이다.

그러나, 실제로 우리가 풀어야 할 무수히 많은 문제들은 선형 함수만으로는 풀 수 없는 비선형성을 갖는 것들이 매우 많다. 그렇다면 선형 문제를 풀기 위해 정의된 하나의 layer를 통해서는 이 비선형 문제를 풀기가 어렵다는 소리가 된다. 이를 풀기 위한 접근법이 다중 레이어를 통한 접근 방법이라 이해하면 좋을 것이다.

좀 더 쉽게 설명하자면, 논리 게이트의 XOR Problem을 보면 좋다. 일반적인 논리 게이트를 AND, OR, NOT에 대한 게이트는 쉽게 볼 수 있는데, XOR 문제의 경우 단일 게이트로 이를 표현하기 어렵다는 문제가 있다. 따라서 XOR 문제를 논리 회로로 표현하기 위해서는 위 그림처럼 OR Gate와 NAND, AND gate들을 잘 조합해야 한다.

직관적으로 위 표와 그래프를 보면 알 수 있을 것이다.

AND, OR 문제에 비해 XOR은 결과값을 선형 그래프로 표현하는 것이 매우 어렵다. 결국 이 문제는 비선형성을 표현하는 문제와도 직접적으로 연결되어 있기도 하다. 다중 레이어 퍼셉트론 구조는 이와 같은 고민에서 출발했다고 볼 수 있다.

기본적인 퍼셉트론 구조의 뉴럴 네트워크는 크게 두 가지 문제를 폴기 위한 목적으로 사용될 수 있다. 하나는 분류(Classification) 문제고 다른 하나는 회귀(Regression) 문제이다. 분류 문제는 입력으로 넣은 데이터가 별도로 정의된 클래스들 중 어느 클래스에 해당하는지 식별하는 문제이며, 회귀 문제는 내가 찾은 어떠한 결과가 특정 정답에 해당하는 어떠한 평면과 얼마나 근접한 가를 찾는 문제로 볼 수 있다. 사실 이와 관련된 부분은 모델 정의 뿐만 아니라 각 문제별로 loss function을 어떻게 정의하느냐에 관한 문제와도 연관되어있다.

기존 MLP 방법의 문제점

MLP 구조의 뉴럴 네트워크의 경우, 일반적인 이미지를 입력으로 받아 연산을 수행하기에는 그 기능이 확장됨에 어려움이 있다. 가장 큰 문제는 학습을 위한 weight의 갯수인데, 이는 입력 이미지의 해상도가 크면 클 수록 기하급수적으로 늘어나게 될 것이다.

예를 들어, CIFAR-10에서 제공되는 이미지처럼 32x32 사이즈의 3채널 이미지가 입력으로 들어오는 경우를 생각해보자. 단일 색상에 대한 픽셀 하나하나가 입력으로 들어간다고 가정할 때, 이 입력이 fully connected layer로 들어가게 되면 하나의 레이어를 거칠 때마다 32 * 32 * 3 = 3072개의 weight를 요구하게 된다. 작은 사이즈의 이미지에서는 이게 문제로 보이지 않을 수 있는데, 만약 입력 해상도가 200x200가 있다고 생각해보자. 그러면 레이어 하나당 200 * 200 * 3 = 120,000개의 weight가 요구된다. 물론 CNN이 본격적으로 image classification 문제를 풀기 위한 솔루션으로 활용되기 시작한 시점에는 224x224 해상도의 영상을 많이 사용했지만, 영상이 HD급 이상으로 올라가게 된다면 한 레이어당 필요하게 되는 weight 갯수개 백만개는 훌쩍 넘어갈 것이고, 이게 또 멀티 레이어로 구성된다면 요구되는 weight 갯수는 감당이 힘들 정도로 늘어날 것이다. weight 수의 증가는 연산량 증가로도 이어질 수 있고, 과적합(overfitting) 문제로까지 이어질 수 있다. 이에 대해서는 다음 포스트에서 자세히 짚어보도록 하겠다.

뿐만 아니라 MLP 구조는 보통 flatten된 1차원 벡터가 입력으로써 들어오게 된다. 이미지가 입력으로 들어왔을 때, 2차원 픽셀로 구성된 이미지를 1차원 벡터 형태로 펴주면 흔히 local 영역에 대한 특성을 잘 잡지 못한다는 문제도 존재하게 된다. 이 문제에 대해서는 CNN의 특징을 보면 왜 문제로 제기되었는지 알 수 있다.

Convolutional Neural Networks

기본적인 CNN 구조는 각각의 히든 레이어가 여러개의 neuron이 1차원 벡터 형태로 쌓여 있는 구조가 아닌 3차원 volume으로 구성되어 있는 구조다. CNN에서는 입력 영상에 대해 각각의 레이어마다 주어진 weight 커널과의 합성곱(convolution)을 수행해 3차원 feature map volume을 출력해주는 구조로, 이미지에 대한 가로, 세로 크기는 줄여가며 각 영역에 대한 특징을 의미론적으로 압축해준 다음 최종적으로 1차원 벡터 형태의 출력을 도출하는 구조다.

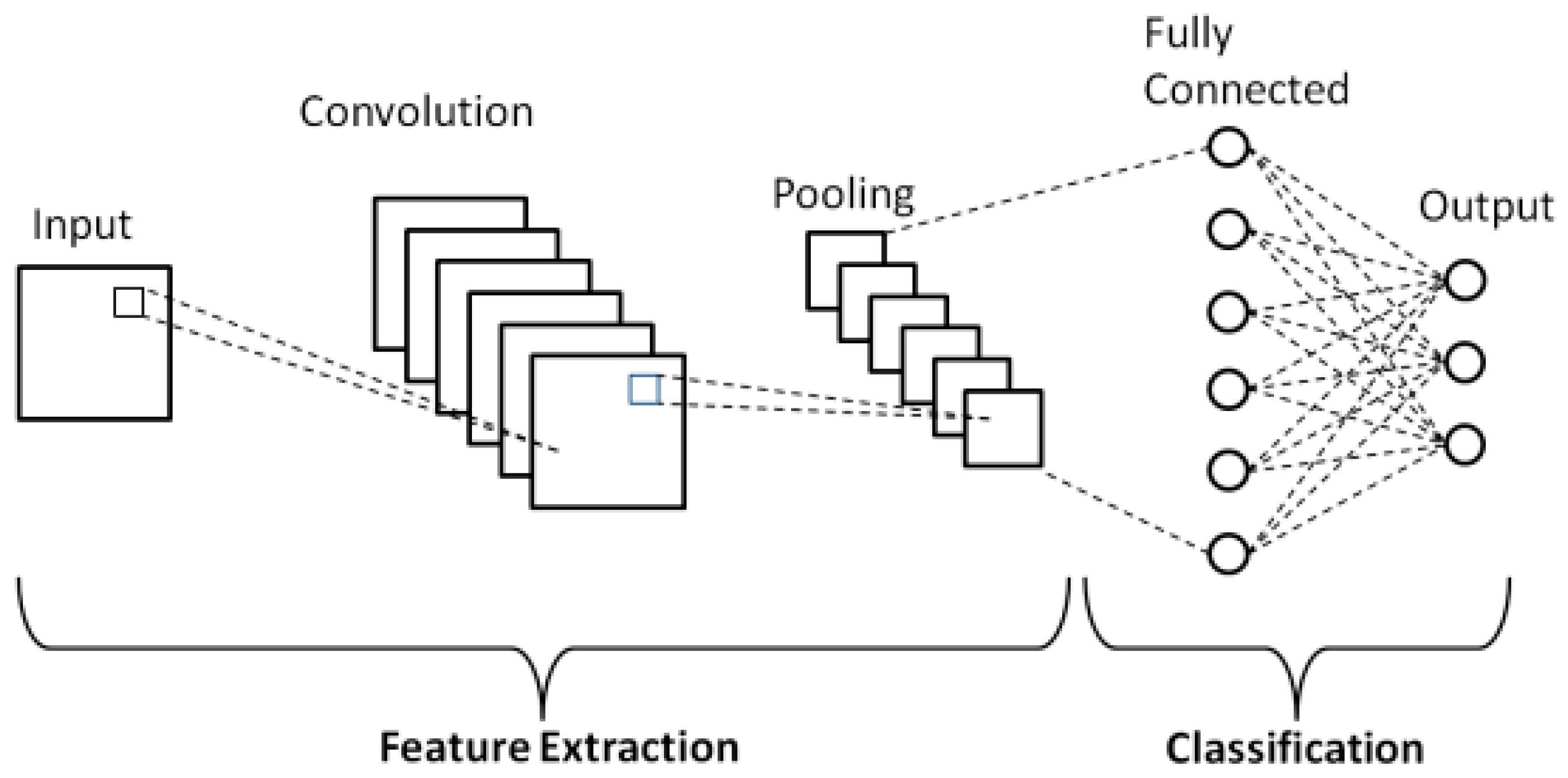
위 그림에 나와있듯이, CNN은 크게 Feature extraction과 Classification 구조로 나뉘어 있다. Feature extraction에서는 상술한 합성곱 과정을 통해 입력 영상의 해상도는 압축되고, 각 픽셀 영역마다 semantic한 정보들을 여러 dimension에 걸쳐 담아주는 feature map을 만들어낸다. 하나의 레이어 내에는 기본적으로 convolution layer, Activation function, Pooling layer로 구성되어 있다.

1. Convolution layer

convolution layer에서는 입력으로 들어온 map과 해당 layer에 주어져 있는 kernel 간 합성곱 연산을 map 전체 영역에 대해 sliding window 형식으로 수행한다. 여기서의 kernel은 weight 값들로 이루어져있는데, convolution layer의 parameter들은 결국 학습이 가능한 weight로 구성된 kernel들의 집합으로 구성되어 있다고 보면 된다. 가령, 우리가 해당 layer를 거치면서 얻고자 하는 다음 feature map의 channel이 32 channel이라면, kernel은 32 channel 만큼 있다는 뜻이 된다. convolution 과정을 통해 우리는 이 layer에서 해당 kernel에 대한 response를 갖는 결과를 얻게 되며, 입력 map으로부터 각 공간적 위치에서 response를 갖는 결과들로 구성된 feature map을 얻을 수 있다. 여기서 나온 feature map에서 활성화 함수(activation function)을 거치고 나면 최종적으로 Activation map을 얻을 수 있다.

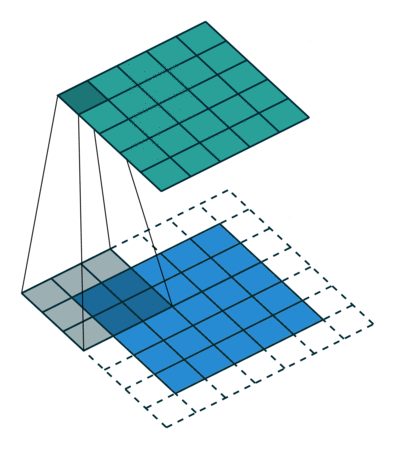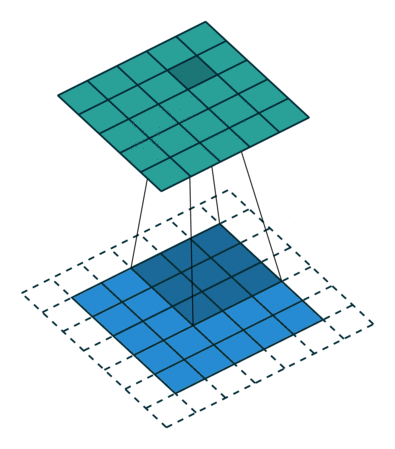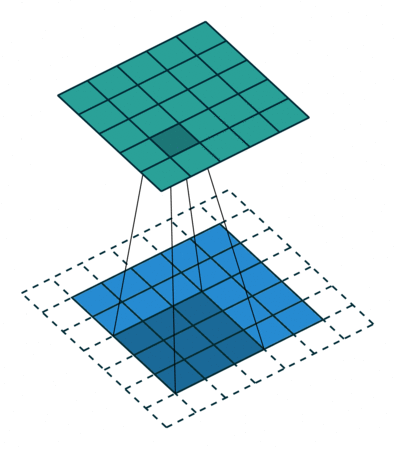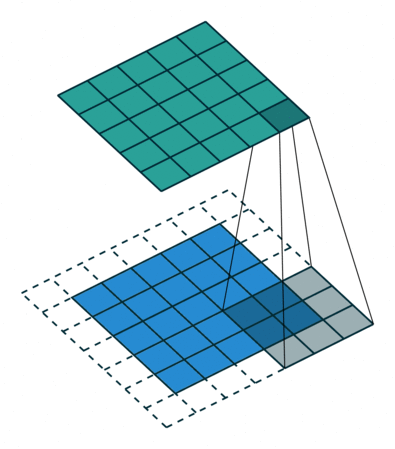
직관적으로 보면 네트워크는 이 kernel을 학습하게 된다는 것을 알 수 있을 것이다. 그럼 각 layer에서의 kernel은 어떠한 response를 얻을 수 있게끔 학습이 될까? 입력 영상이 하나 들어온다고 가정했을 때, 초반부 layer에서는 초기 입력 영상과 유사한 스케일의 map을 얻게 될 테니 영상 내 local한 영역에서의 edge나 pattern 등에 대한 부분을 보며 response가 발생하는 activation map을 얻을 것이다. 후반부로 갈 수록 output map의 width와 height는 입력 대비 많이 작아질 것이다. 반복적인 convolution 연산을 통해 이제 activation map은 초반부 대비 local한 영역에서의 response에는 주목할 수 없고, 픽셀 영역 하나하나가 이전보다 더 추상적이고 semantic한 정보를 담는 형태로 map을 만들어낼 것이다. 이러한 특성 때문에 초반부 convolution layer에서는 local한 위치에서의 response에 주목할 수 있게 되고(흔히 이 case를 localization이라고 이야기하는 경우가 많았습니다.), 후반부 layer에서는 semantic한 정보에 대한 response에 주목할 수 있게 될 것이다. 아마 이 내용을 보면 CNN이 결국 나중에는 위치 정보에 대한 취약점이 있지 않을까 하는 의문이 들 수 있는데, 이와 관련해서는 차후에 언급하도록 하겠다.

그렇다면 이러한 convolution layer를 왜 쓰는지에 대한 이해가 필요한데, 과연 convolution layer는 fully connected layer 대비 어떠한 강점을 가지고 있는 것일지 알아보도록 하자.

Local connectivity

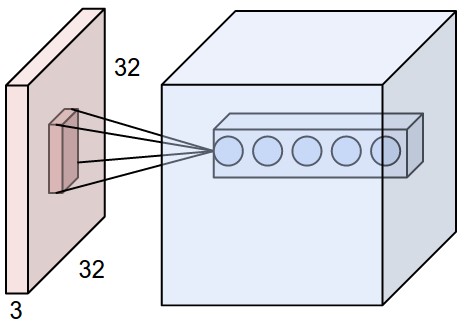
Convolution 연산은 작은 사이즈의 kernel을 기반으로 연산을 수행한다. 이로 인해 각각의 convolution 연산 결과는 입력으로부터 지역적으로 인접한 부분끼리만 연결되어 그 결과를 도출한다. 여기서 이 지역적으로 인접한 부분에 대한 공간적인 범위를 Receptive field라고 한다. 쉽게 말하면 사실상 kernel size와 동일하다고 보면 되는데, output map의 한 영역이 다루는 내용은 input map 내 유사한 위치에서 kernel size만큼의 영역이라고 이해하면 될 것이다.

예를 들어, 32 x 32 x 3 크기의 입력이 들어왔다고 가정해보자. 여기에 우리는 원하는 feature map을 얻기 위해 5 x 5 x 5 크기의 kernel을 이용해 convolution 연산을 적용한다. kernel의 channel이 5이기 때문에 출력의 한 영역에는 5개의 neuron 값을 갖게 될 것이고, 이 5개의 neuron들은 5 x 5 x 3 영역에 대한 weight를 기반으로 그 값을 얻어낼 것이다. 결과적으로 이 5개의 neuron은 동일한 receptive field 영역을 보게 될 것이다.

Spatial arrangement

그렇다면 과연 convolution 이후의 output layer에는 몇 개의 neuron이 어떤 형태로 배열되어 있을까?

output layer의 크기를 좌우하는 요인으로는 kernel의 size(f)와 channel(K)과 stride(s), 그리고 padding(p)이 있다. 여기서 stride는 kernel을 sliding하면서 연산을 할 때, 그 sliding의 step을 의미하는 hyper-parameter이고, padding은 입력의 가장자리 영역을 0 값으로 채워 입력 대비 output layer의 크기가 줄어들지 않을 수 있는 역할을 하는 hyper-parameter다. 이를 토대로 보통 output layer의 크기는 ( ( (w - f + 2p) / s) + 1) x ( ( (h - f + 2p) / s) + 1) x K 라고 정리할 수 있다. (여기서, w와 h는 input의 width와 height를 의미합니다.) 문제는 이 공식이 맞는 공식인지가 확인이 필요하다.

1차원의 입력과 kernel이 있다고 가정해보자. 이 그림을 보면 kernel의 크기가 3으로 할당되어 있고, input의 크기가 7인 것을 확인할 수 있다. 여기서 입력의 양 끝단이 0인 것을 볼 수가 있는데, 이는 입력에 padding 값을 주었기 때문이다. 따라서 이 입력은 padding=1이라는 설정 하에 양 끝단에 padding을 준 입력 값이라는 것을 알 수가 있고, 결론적으로 우리는 원본 input은 크기가 5라는 것을 확인할 수 있다. 그림의 왼쪽을 보면 sliding step이 한 칸씩 진행되는 연산임을 볼 수가 있어 여기서 설정된 stride는 1이라는 것도 확인되었다. 그럼 이제 이 값들을 토대로 위에서 언급한 공식에 대입해보자.

결과적으로 그림의 왼쪽과 같이 값이 5가 나왔으니 이 공식이 성립함을 알 수가 있다. 마찬가지로 그림의 오른쪽 부분대로 stride를 2로 주면 공식에 따라 output 크기 값이 3이라는 것도 확인되었다.

여기서 주의해야 할 점은 위에 언급한 hyper-parameter 들은 상호간에 연관성이 있다는 점이다. 하나의 예로 크기가 10인 1차원 input이 들어왔다고 해보자. 여기서 hyper-parameter 값들이 f = 3, p = 0, s = 2라고 해보자. 공식대로 대입을 하면 (((10 - 3) / 2) + 1) = 4.5가 나오게 된다. 이 말은 즉, 공식대로 계산을 하면 output size가 자연수가 나오지 않는다는 문제가 발생한다. 소숫점이 나왔다라는 것은 결론적으로 나눗셈 연산이 들어가는 stride 쪽의 영향이 크게 작용했다라는 것을 알 수가 있는데, 이 때문에 나머지 hyper-parameter 값들에 따라 stride 값을 잘 주어야 한다는 제약 사항이 생기게 된다.

Parameter sharing

Parameter sharing은 CNN의 특장점 중 하나다. 하나의 kernel map을 이용해서 영역별로 sliding window 형태로 계산을 하기 때문에 입력의 각 영역별로 서로 다른 weight를 준비해야하는 부담이 덜하게 된다. 여기서 kernel의 channel이 32라고 하면, kernel에는 32개의 unique한 weight set을 갖는다고 볼 수 있다. CS231n 블로그 내에 적힌 설명을 보면 전체 layer 중 하나의 channel에 있는 하나의 slice를 depth slice라 이야기하고 있다. 가령 55 x 55 x 64의 map이 하나 있다고 가정하면 이 map은 55 x 55 크기의 depth slice가 64장이 있는 것이다. 단위를 이와 같이 나누어 설명하자면, 각각의 depth slice에 있는 모든 뉴런들은 kernel 내에 있는 같은 파라미터들을 사용한다고 이해하면 된다.

위 그림은 AlexNet에서 첫 convolution layer에 사용하는 96개의 11 x 11 x 3 필터들이라고 한다. 그림을 보면 대각 성분에 대한 필터를 갖기도 하고, 어떤 패턴처럼 생긴 필터나 색상 변화를 나타내는 필터 등등… 그 각각의 필터들이 주목하는 특성들을 알 수가 있다. 첫 번째 필터를 예를 들어보자. 입력 영상의 어떠한 영역에서 이 첫 번째 필터를 넣었을 때, 중요한 결과가 나온다면 이는 이미지 상 다른 위치에서도 유용해야만 한다. 이는 보통 이미지가 Translationally-invariant한 구조를 갖기 때문이라고 하는데, 이로 인해 위 사진의 첫 번째 필터에 대해 관련된 성분을 검출하기 위해 모든 이미지 영역에 대해 일일히 parameter를 재학습할 필요가 없음을 의미한다. 특히, 입력 이미지가 특정한 중심 구조를 가지는 경우, 이미지의 다른 면에서 완전히 다른 특징을 학습해야 한다는 이야기도 있다. 사실 이 구절만을 직역해서 읽어보면 무슨 이야기인지 알기가 쉽지 않았는데, 이미지 중앙에 얼굴이 있는 입력 이미지를 예로 들어서 생각해보았다. 외형적으로 사람의 눈과 머리는 다른 위치에 있다라는 것을 우리는 직관적으로 알 수 있다. 따라서 하나의 필터를 통과한다면 눈에 특화된 특징과 머리에 특화된 특징은 공간적으로 각각 다른 위치에서 학습되어야만 할 것이다. 이는 즉, 이미지가 지역적인 부분마다 다른 특화된 특징을 내놓을 수 있어야 한다는 것을 의미한다고 볼 수 있고, 이러한 부분 때문에 Convolution layer는 locally-connected layer라고도 할 수가 있다. &&

요약하자면,

2. Pooling layer

CNN에서는 이전 레이어에서 연산된 결과 map을 토대로 정보를 좀 더 모아 이전 레이어 대비 더 작은 사이즈로 down-sampling하는 목적으로 pooling layer를 사용한다. 특히, 초창기 CNN이 나오던 시기에는 convolution layer 사이사이에 pooling layer를 넣는 것이 거의 공통적이기도 했다. Pooling layer를 사용하게 되면 down-sampling 효과를 가져올 뿐만 아니라 이로 인해 네트워크 계산량과 파라미터 수를 줄여주기도 하고, 파라미터 갯수가 줄기 때문에 오버피팅 컨트롤 역할도 할 수 있다는 주장도 있다(아무래도 파라미터 갯수와 오버핏팅의 상호 관계에서 비롯된 이야기이지 않을까 싶습니다. 오버핏팅에 관한 이야기는 차후에 자세히 다루어 보겠습니다.). 이러한 Pooling layer는 각각의 depth slice에서 독립적으로 동작한다. 따라서 입력의 channel에는 영향을 주지 않으며, 입력에 대해 고정된 함수를 사용하기 때문에 별도의 파라미터도 없고, padding 값도 따로 할당하지 않는다.

대표적으로는 Average pooling과 Max pooling을 사용한다. Average pooling은 pooling을 적용할 filter 크기 내에 속한 값들의 평균을 output으로 출력하는 방법이고, max pooling은 이들 중 가장 큰 값을 output으로 출력하는 방법이다. pooling 방법에 대한 추세를 보면 오래 전에는 average pooling을 자주 사용해왔지만, 선호도가 차츰 max pooling으로 치우쳐갔다고 한다. 더 나중의 이야기인데, 이 max pooling도 사실상 영역 내 최댓값만 보기 때문에 다른 값들은 보지 않게 되어 이로 인해서 또 오버핏팅이 야기하는 경우도 있었다고 한다. 나중에 Pooling layer 자체를 제거하기 시작한 이유이기도 한데, 이에 관해서는 후발 연구들을 보며 확인을 해야겠다.

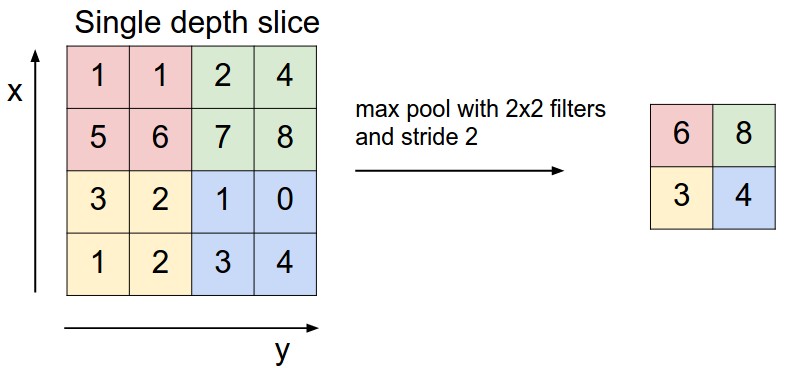
Pooling layer의 back-propagation

위 그림은 Max pooling의 역전파 과정을 나타낸다. 뒷 레이어로부터 역전파된 gradient 값이 각각 delta_1, delta_2라고 할 때, 역전파를 통해 이전 영역으로 전파된 값을 delta_11, delta_12, delta_21, delta_22라고 하자. 그림 상에서는 max pooling이 두 개의 neuron으로부터 나온 결과로 표현되어 있다. 즉, max pooling은 두 개의 neuron 값 들로부터 가장 큰 값을 가져오게 된다는 말이다. 만약 윗 neuron 값이 max 값이어서 해당 값만을 pooling을 통해 가져왔다면 아랫 neuron은 사실상 의미가 없는 값이나 다름없게 된다. 따라서 이 pooling에 대해 반대로 역전파를 하게 되었을 땐 max 값이 있던 neuron에 대해서만 local gradient 가중치를 1로 주어 이전 delta 값을 역전파시키고, 다른 neuron에 대해서는 local gradient 가중치를 0으로 주어 이전 delta 값을 역으로 전달하지 않게 된다. (사실 이 부분을 읽으면서 들었던 의문점은 max 값이 어디서부터 온 것인지 그 위치에 대한 정보도 결국 기억해야 하는가라는 의문이 생겼습니다. 제가 그 과정 하나하나에 대한 이해가 짧아서 그럴 수 있는데, 아시는 분 댓글로 알려주시면 감사하겠습니다 ㅠㅠ)

반대로 average pooling은 평균 값을 기반으로 pooling을 수행하기 때문에 local gradient 값도 전체 neuron 갯수를 나눈 만큼이 된다. 평균을 구하는 공식이 있다고 할 때, 평균 공식에 대해 미분을 하면 결국 1/m만 남기 때문이다. 당연하겠지만, 단순히 뒷 레이어로부터 나온 gradient 값에 local gradient 값만 곱하면 나온다고 정리가 된 이유는 Back-propagation이 Chain rule 원리에 따라 값이 전파되기 때문이다.

3. Fully connected layer

앞 단에서 feature map을 만들어내면 해당 map이 classification을 위한 fully connected layer에 입력으로 들어가 최종적으로 하나의 vector를 만들어낸다. 이 vector는 최종적으로 풀고자 하는 classification에 대한 class 갯수만큼, 그 class 각각의 확률을 의미하는 값을 포함하고 있다. 기본적인 구조 자체는 Multi layer perceptron과 유사하기 때문에 자세한 설명은 생략하도록 하겠다.

4. Basic architecture

기본적으로 CNN 내에서의 convolution layer는 convolution 연산을 위한 kernel과 activation function 순서로 구성되어 있다. 이 뒤에 필요에 따라 pooling layer가 붙는 구조다. Activation function에는 보통 ReLU를 많이 쓰는 편인데, 목적에 따라 Leaky ReLU, ELU 등등 여러 선택지가 있다. Feature extraction을 수행하는 부분에서는 이러한 [Conv - ReLU - Pool] 구조가 반복적으로 배치되어 최종적으로는 입력 영상 대비 가로, 세로 크기가 많이 줄어들고 그 각각에 semantic한 특징을 내포하고 있는 feature map을 만들어낸다. 어느 정도 원하는 크기의 feature map을 얻게 되면 여기 있는 값들을 flatten시켜 1차원의 vector꼴로 변환하는데, 이 vector 형태의 입력이 여러 차례의 fully connected layer를 거치고, 최종적으로 class score를 출력해준다. 여기서의 class score는 우리가 classification 문제를 풀기 위해 사전에 정의한 class들에 대해 해당 영상이 특정 class에 해당할 확률을 나타낸다. 기본적인 예제에서는 1000개의 값을 갖는 class score vector를 출력한다고 설명이 되어있는데, 이는 1000개의 class에 대한 classification 확률을 뽑기 위함이라고 보면 된다.

조금 더 살펴보자면, CNN의 전체 구조는 보통 다음과 같은 흐름으로 되어있다 볼 수 있다.

1번과 같은 구조는 여러 레이어가 쌓여 있는 형태가 아니기 때문에 보통 선형 분류에 대한 문제를 풀 때 사용할 수 있는 간단한 구조다. 3번과 4번 구조가 기본적으로 다수의 [Conv - ReLU - Pool] 구조가 반복되는 형태인데, 4번이 3번과 달리 Conv - ReLU가 한 차례정도 더 나오고 Pooling을 진행하는 구조로 되어 있다. 이는 다수의 convolution layer를 통과했을 때, 더 복잡한 feature를 얻을 수 있다는 이점이 있기 때문이다. 이런 다음에 pooling을 진행하면 동일하게 down-sample된 feature map에 대해 3번보다 더 복잡한 특징 정보들을 많이 얻을 수 있을 것이다.

각 파트에 대해 빠진 설명들이 일부 존재하는데, 이는 다음 포스트를 통해 추가로 언급해보도록 하겠다.